The Most Useless Pi Algorithm

Intro

There are many algorithms for computing pi, ranging from the fiercely efficient Ramanujan formulae that can become thirty orders of magnitude more accurate with each additional term in the expansion, to the familiar but plodding result from the power-series expansion of arctan(1), for which more detail is here.

This page is concerned not with finding a more efficient way to compute pi, since one would need to be extremely intelligent to do better than all the clever mathematicans who have worked on it.

Uselessness:

A Cost-Benefit Analysis

Enough with efficiency! This page describes a candidate for the most useless way of computing pi. Let us define this concept more closely with a cost-benefit analysis: I shall define uselessness in terms of high cost, both computational and intellectual, and in terms of zero or negative benefit. The algorithm discussed below, you may be assured, provides a highly negative benefit and high initial cost.

The idea is to take a million or so digits of pi that have been computed by somebody else, and use these to extract an extremely inaccurate approximation to pi.

We could of course take the million digits and strip off 999,999 of them, but we can also do better, by adding considerable intellectual and computational cost to arrive at the approximation.

The Algorithm

The algorithm is based on the following two ideas:

The probability of two large random integers being coprime (having no common factor) is 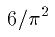. A proof of this, using the magnificent Riemann zeta function, is lots of fun.
The digits of pi form a random sequence. I have no proof of this, and neither does anyone else, because it is patently not true: the digits of pi are very definite and well-defined, not random. Perhaps a better statement would be that the digit sequence passes all known tests for randomness.

The algorithm is then this:

Take N digits of the decimal expansion of pi to serve as a pool of random digits. From these take samples of pairs of n-digit numbers. Count the number of coprime pairs, and after K samples derive an estimate of the probability of a pair being coprime, which is thus an estimate for 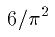, and hence we can estimate pi itself.

If N, n and K are all infinite (ha ha) then the result for pi is exact, and the trick in running this algorithm practially is in choosing these numbers a ppropriately. I used the value of pi from Project Gutenberg, with N=1250000 digits. The way to tell if two numbers are coprime is by the Euler method. I used successive sequences of 6-digit numbers until they ran out, so that the first few samples are:

314159 265358 coprime
979323 846264 not coprime (common factor is 3)
338327 950288 coprime
419716 939937 coprime
510582  97494 not coprime (common factor is 6)
459230 781640 not coprime (common factor is 10)
628620 899862 not coprime (common factor is 6)

The final result is that of the 104000 pairs of random 6-digit numbers, 63022 of them were coprime, so that we (uselessly) conclude that pi is approximately sqrt(6*104000/63022), which is:

pi = 3.146634

which is really pretty useless I think, considering that the only thing we started with was a value of pi accurate to over a million decimal places.

Acknowledgement

I would like to thank Robert A. J. Matthews of the University of Aston in England, who had the idea of using coprimality of random integers to compute pi. See "Nature", vol 374, page 681, April 20, 1995.